ELEARNING - FREIBURG

HOME   Mathematik   Prüfungsaufgaben

♦ Abikurs Mathe - Stochastik ♦

<< 06 - Erwartungswert >>

Erwartungswert

Im Zusammenhang mit Zufallsvariablen gibt es gewisse Kenngrößen, mit denen man sich eine ungefähre Vorstellung über die zugehörige Wahrscheinlichkeitsverteilung machen kann. Bei diesen Kenngrößen handelt es sich um den Erwartungswert, die Varianz und die Standardabweichung. In diesem Abi-Kurs beschäftigen uns ausschließlich mit dem Erwartungswert,

Formal ist der Erwartungswert E(X) einer Zufallsvariablen X wie folgt definiert:

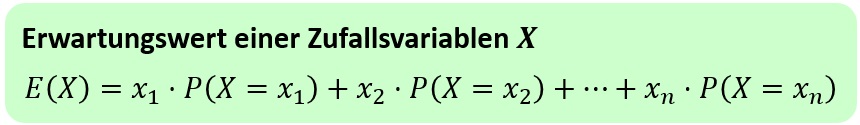
Wir können diese Formel in Worten etwa wie folgt verstehen. Eine Zufallsvariable X kann gewisse Werte x1, x2 bis xn annehmen. Die Wahrscheinlichkeit, dass X den Wert xi annimmt ist P(X=xi). Das Produkt xi·P(X=xi) verleiht dem Wert xi nun ein gewisses Gewicht.
Der Wert xi trägt also nur zu einem gewissen Anteil zu der obigen Summe bei. Insofern dürfen wir den Erwartungswert als den "gewichteten" Mittelwert der betreffenden Wahrscheinlichkeitsverteilung ansehen.

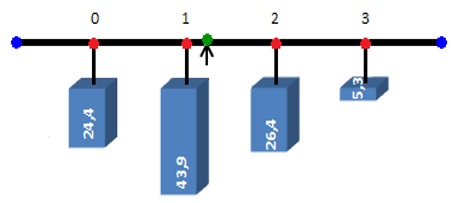
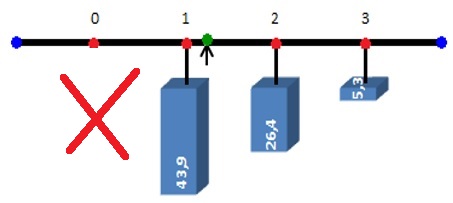
Dies lässt sich auch mit gewissen Einschränkungen einem Bild veranschaulichen. Wir denken uns einen Stab, der für jeden Wert einer Zufallsvariablen X eine Markierung enthält. An jeder Markierung hängt ein Gewicht, das der jeweiligen Wahrscheinlichkeit entspricht. Die Stelle des Schwerpunkts bzw. Gleichgewichtspunkts nennt man den Erwartungswert.

Aber wie gesagt, hier gibt es einen kleinen Haken. In der Abbildung gibt es nämlich eine Markierung 0, an der ein Gewicht hängt. Da laut der obigen Definition aber das Produkt 0·P(X=0) gebildet werden muss und dieses mit dem Wert 0 (also gar nicht) zu der obigen Summe beiträgt, dürfen wir an unseren Stab kein Gewicht an die Markierung 0 hängen. Andernfalls wird man von einer solchen Abbildung leicht in die Irre geführt.

In den Prüfungsaufgaben wird der Erwartungswert häufig in Zusammenhang mit dem Ausgang eines Spiels abgefragt. Man soll dann beantworten, ob ein Spiel fair ist oder nicht bzw. für welche Partei das Spiel günstiger ist.

Rechenbeispiel 1

Eines der folgenden fünf Wörter werde zufällig gezogen:

DER ZUFALL REGIERT DIE WELT

Die Zufallsvariable X beschreibe die Anzahl der Buchstaben und die Zufallsvariable Y die Anzahl der Vokale des gezogenen Wortes. Bestimmen Sie die Erwartungswerte der beiden Zufallsvariablen.

Lösung

X kann die Werte 3, 4, 6 oder 7 annehmen. Der Satz DER ZUFALL REGIERT DIE WELT hat 5 Worte, von denen zwei die Länge 3 haben. Also folgt P(X=3) = 2/5 = 0,4. Entsprechend gilt: P(X=4) = 1/5 = 0,2, P(X=6) = 1/5 = 0,2 und P(X=7) = 1/5 = 0,2. Der Erwartungswert ergibt sich dann durch:

E(X) = 3·0,4 + 4·0,2 + 6·0,2 + 7·0,2 = 4,6

Die Zufallsvariable Y kann die Werte 1, 2, oder 3 annehmen. Mit P(Y=1) = 2/5, P(Y=2) = 2/5, P(Y=3) = 1/5 folgt:

E(Y) = 1·2/5 + 2·2/5 + 3·1/5 = 9/ 5 = 1,8

Ergebnis: Die gesuchten Erwartungswerte sind E(X)=4,6 und E(Y)=1,8. Das bedeutet, dass man (bei langen Versuchsreihen) im Schnitt eine Wortlänge von 4,6 erhält und dass ein Wort im Schnitt 1,8 Vokale besitzt.

Rechenbeispiel 2

Bei einem Spiel wird ein Würfel zweimal hintereinander geworfen. Der Spieler gewinnt 2 €, wenn er einen Pasch (=zweimal dieselbe Zahl) geworfen hat.

a) Berechne den erwarteten Gewinn!
b) Berechne, wie groß der auszuzahlende Betrag im Gewinnfall sein müsste, damit bei einem Einsatz von 1 € das Spiel fair ist!

Lösung

a) Hier stellt die Zufallsvariable X den Gewinn dar. Der Spieler gewinnt 0 €, wenn er zwei verschiedene Zahlen wirft und 2 €, wenn er einen Pasch wirft. Demnach ist P(X=0) = 30/36 = 5/6 und P(X=2) = 6/36 = 1/6. Der erwartete Gewinn ist dann E(X) = 0·5/6 + 2·1/6 = 1/3 = 0,33.

Ergebnis: Der erwartete Gewinn beträgt etwa 33 Cent.

b) Ein Spiel ist dann fair, wenn der erwartete Gewinn genauso hoch ist wie der Einsatz, d.h. wenn E(X)=1 gilt. Den Auszahlungsbetrag a im Gewinnfall berechnen wir dann mit E(X) = 0·5/6 + a·1/6 = 1, woraus a=6 (Euro) folgt.

Ergebnis: Damit das Spiel fair wird muss der Auszahlungsbetrag im Falle eines Gewinns auf 6 € festgelegt werden.

Downloads

PowerPoint
PDF